Математические формулы для приготовления балансировочных программ в домашних условиях.

В этом случае количество исходных уравнений становиться больше, чем количество неизвестных. Для получения однозначного решения нужно придумать что-то этакое, которое объединяло бы все неизвестные общим условием. Гаусс изобрел метод наименьших квадратов (МНК), с помощью которого можно было получать однозначные решения для специфических задач в разных областях знаний. Использовали его и балансировщики.

Корректирующие грузы, вычисленные методом наименьших квадратов, обеспечивают минимальные остаточные вибрации во всех точках измерения (в данном случае более двух). Остаточные вибрации будут разными, но минимальными для каждой индивидуальной точки.

Далее приведены формулы, с помощью которых можно в Excel составить программу вычисления балгрузов этим методом. Итак, поехали, не пугайтесь!

       (7.1)

где:

 - составляющая по оси X балгруза    для 1-й плоскости

 - составляющая по оси Y балгруза    для 1-й плоскости  

 - составляющая по оси X балгруза    для 2-й плоскости  

 - составляющая по оси Y балгруза    для 2-й плоскости  

 - определители, которые вычисляются по формулам (7.2)

 - определитель знаменателя по формуле (7.3)

Определители числителей выглядят следующим образом:

       (7.2)  

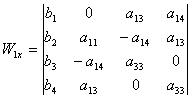
Определитель знаменателя таков:

  (7.3)

Следует обратить внимание на свойство определителя знаменателя: сумма элементов первой колонки равна сумме элементов первой строки; сумма элементов второй колонки равна сумме элементов второй строки и т.д.

Действительно:

колонка  равна строке .  

Элементы определителей вычисляются по формулам (7.4-7.9), где все члены определителей являются просто числа (не вектора, точки над индексом нет):  

  (7.4)

  (7.5)

  (7.6)

  (7.7)

Элементы с индексом  вычисляются по формулам (7.8)

Многоточие означает, что цепочки сумм могут быть продолжены в том же стиле в случае большего количества точек измерения (F, G, H и т.д.).

Составляющие Квл этих сумм по оси X и по оси Y означают:

 - составляющая по оси X вектора  (или вещественная его часть)  

 - составляющая по оси Y вектора  (или мнимая его часть)  

 - составляющая по оси X вектора  (или вещественная его часть)  

 - составляющая по оси Y вектора  (или мнимая его часть)  

 - составляющая по оси X вектора  (или вещественная его часть)  

 - составляющая по оси Y вектора  (или мнимая его часть)

 - составляющая по оси X вектора  (или вещественная его часть)  

 - составляющая по оси Y вектора  (или мнимая его часть) 

И так далее, для точек C и D.

 - составляющая по оси X исходного вектора вибрации 

 - составляющая по оси Y исходного вектора вибрации   

 - составляющая по оси X исходного вектора вибрации   

 - составляющая по оси Y исходного вектора вибрации   

 - составляющая по оси X исходного вектора вибрации   

 - составляющая по оси Y исходного вектора вибрации   

 - составляющая по оси X исходного вектора вибрации   

 - составляющая по оси Y исходного вектора вибрации   

Составляющие по осям X и Y указанных выше величин вычисляются по формулам (7.9)

Составляющая по оси X -    (7.9)

Составляющая по оси Y -  

Где    амплитуда вектора,    аргумент (фаза) вектора.

Так, например,         

 - амплитуда вектора коэффициента влияния 

 - фаза вектора коэффициента влияния   

Небольшое отступление. Вычисление балгрузов при балансировке в двух плоскостях по двум точкам можно выполнить и методом наименьших квадратов, но при этом конечные формулы будут такими же, как и при классическом методе (пункт 1). Таким образом, метод наименьших квадратов не устраняет трудностей при вычислении балгрузов при балансировке в двух плоскостях по двум точкам.

Действительно, ниже приведена формула для вычисления подкоренного выражения знаменателя при балансировке методом наименьших квадратов при балансировке в двух плоскостях для четырех точек (ABCD).

Кстати, ее можно продолжить и для большего количества точек в том же стиле. Так вот, из этой формулы получается, что при балансировке в двух плоскостях и для двух точек, т.е. когда все остальные коэффициенты влияния равны нулю, а именно:

знаменатель становится равным:

Таким образом, при балансировке в двух плоскостях по двум точкам вычисление балгрузов производится по одним и тем же формулам, как при классическом способе (пункт 1), так и методом наименьших квадратов.

Автор rotkiv