Математические формулы для приготовления балансировочных программ в домашних условиях.

Предисловие. Эти формулы общеизвестны. Просто использовал их для построения в Excel математической модели объектов балансировки. Около 30% объектов в моей практике оказывались мудреными, и упомянутая модель помогала мне их распутывать. Формулы пригодны только для жестких роторов и линейных объектов. Матмодель выдавала результаты, которые чуть-чуть не совпадали с результатами прибора AU-014, что меня вполне устраивало.

Исходные формулы (1.1). Это просто система из двух алгебраических уравнений первой степени с двумя неизвестными, правда, в комплексном виде. Все величины векторные, о чем свидетельствует точка над индексом.  

      (1.1)  

Решив эту систему, получаем формулы (1.2.) для вычисления балансировочных грузов.

        (1.2.)

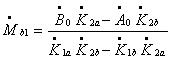
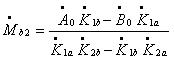
где:

 - дисбаланс в 1-й плоскости (масса в граммах, угол в градусах)

 - дисбаланс во 2-й плоскости (масса в граммах, угол в градусах)

 - корректирующий (балансировочный) груз для 1-й плоскости  

 - корректирующий (балансировочный) груз для 2-й плоскости  

 - величина исходной вибрации в точке А (при нулевом пуске)

 - величина исходной вибрации в точке В (при нулевом пуске)

 - коэффициент влияния 1-й плоскости на точку А

 - коэффициент влияния 1-й плоскости на точку В  

 - коэффициент влияния 2-й плоскости на точку А  

 - коэффициент влияния 2-й плоскости на точку В  

Формулы для вычисления коэффициентов влияния см.ниже (1.2.1 и 1.2.2.)

Знаменатель обозначим строчной латинской буквой   

    (1.3.).  

Знаменатель  – есть разность произведений коэффициентов влияния. Если знаменатель близок к нулю, то возникает проблема корректности выбора балансировочных плоскостей. Одна из причин низкой балансируемости объекта носит название «слияние балансировочных плоскостей».

Автор rotkiv