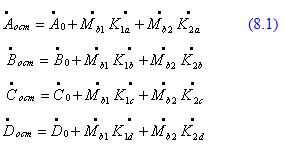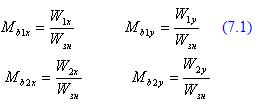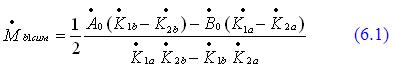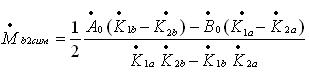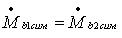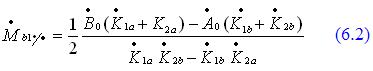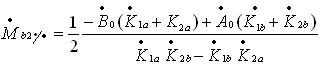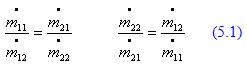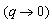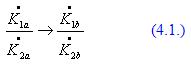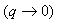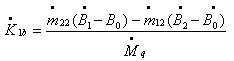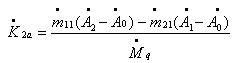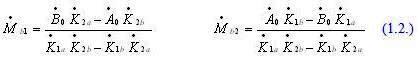Вибродиагностика это метод неразрушающего контроля для диагностики агрегатов, в основе которого лежит анализ измеренного уровня/значений вибрации, которая является проявлением определенного/предполагаемого дефекта или неисправности какого-либо узла данной машины. Вибродиагностика позволяет оценить техническое состояние агрегата в режиме его эксплуатации. При проведении вибрационной диагностики проводится исследование виброскорости (мм/с), виброперемещения (мкм), виброускорения (мм/с2) с помощью спектрального анализа или сигнала по времени.
Вибродиагностика широко используется для оценки технического состояния подшипников качения, подшипников скольжения, паровых и газовых турбин, электродвигателей/генераторов, компрессорных установок, насосного оборудования, редукторов и мультипликаторов.
Вибрационная диагностика обнаруживает скрытые дефекты оборудования без демонтаж/монтажа элементов агрегата. Непосредственно сам процесс снятия вибрационных характеристик занимает небольшое время по продолжительности, но предъявляет некоторые особые требования к установке вибродатчика.

Векторы остаточных вибраций вычисляются по следующим формулам:

Формулы могут быть продолжены в том же стиле в случае большего количества точек измерения (F, G, H и т.д.).

Где:

И так далее для точек C и D.
При вычислении уравновешивающих грузов  методом наименьших квадратов остаточные вибрации во всех точках измерения (A, B, C и D) будут минимальными.

В этом случае количество исходных уравнений становиться больше, чем количество неизвестных. Для получения однозначного решения нужно придумать что-то этакое, которое объединяло бы все неизвестные общим условием. Гаусс изобрел метод наименьших квадратов (МНК), с помощью которого можно было получать однозначные решения для специфических задач в разных областях знаний. Использовали его и балансировщики.

Корректирующие грузы, вычисленные методом наименьших квадратов, обеспечивают минимальные остаточные вибрации во всех точках измерения (в данном случае более двух). Остаточные вибрации будут разными, но минимальными  для каждой индивидуальной точки.
Далее приведены формулы, с помощью которых можно в Excel составить программу вычисления балгрузов этим методом. Итак, поехали, не пугайтесь!

где:

                        
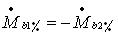
(груз во второй плоскости противоположен по фазе, сдвинут на 180 градусов)

Знаменатель в формулах (2.1) вычисляется по формуле (2.2)

                                      
Это векторная разность двух произведений, составленных из четырех  векторов.
Где:

Если 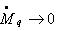 , то пробные грузы выбраны не корректно.

Признак «качельности» объекта 

Признак слияния плоскостей балансировки 

Если при каждом пуске пробные грузы устанавливаются в обеих корректирующих плоскостях, то  коэффициенты влияния вычисляются по формулам   (2.1.).
                        

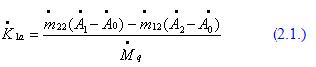
Исходные формулы   (1.1). Это просто система из двух алгебраических уравнений первой степени с двумя неизвестными, правда, в комплексном виде. Все величины векторные, о чем свидетельствует точка над индексом.
        

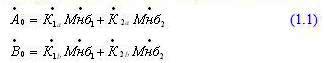
Решив эту систему, получаем формулы (1.2.) для вычисления балансировочных грузов.

         
где:

Формулы для вычисления коэффициентов влияния см.ниже (1.2.1 и 1.2.2.)