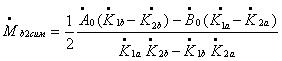Математические формулы для приготовления балансировочных программ в домашних условиях.

Где: , а фаза вектора произведения равна   

Где: , а фаза вектора, равного частному от деления двух векторов, равна

Автор rotkiv

Математические формулы для приготовления балансировочных программ в домашних условиях.

 или  

Дано: , найти  и 

 Автор rotkiv

Математические формулы для приготовления балансировочных программ в домашних условиях.

Точки над условным буквенным обозначением векторов означают, что рассматриваемые величины векторные, т.е. они имеют не только величину (амплитуду), но и направление (фазу). Более подробное и равноценное обозначение векторных величин такое:

Где,

 - фазы соответствующих векторов, угол направления вектора относительно положительной оси X в декартовой системе координат. Сложение, вычитание векторных величин может быть только геометрическое.

Но есть и аналитические формулы для сложения и вычитания векторов. Амплитуда суммы (разности) векторов и тангенс его фазы вычисляются по формулам:

Математические формулы для приготовления балансировочных программ в домашних условиях.

 Для того, чтобы выполнять действия воспользоваться инженерными формулами векторного калькулятора.

Для того, чтобы использовать Excel для выполнения математических операций над векторами, необходимо векторную форму преобразовать в комплексные числа.

 Формулы преобразования вектора в комплексное число:

где:

 - амплитуда (скз, размах) вибрации  

 - фаза вибрации в градусах

 - фаза вибрации в радианах

 - мнимая единица (не обращай внимания, Excel все берет на себя).

Математические формулы для приготовления балансировочных программ в домашних условиях.

Эффективность снижения первоначальной (исходной) вибрации после проведения балансировочных работ обозначим буквой  вычисляется по следующей формуле (формулу подарил Тараканов Вячеслав Михайлович)

 %  

Поскольку для оценки эффективности балансировки направление векторов остаточной вибрации не играет решающей роли, то в формуле задействованы только остаточные амплитуды векторов.

Автор rotkiv

Математические формулы для приготовления балансировочных программ в домашних условиях.

Векторы остаточных вибраций вычисляются по следующим формулам:

  (8.1)

Формулы могут быть продолжены в том же стиле в случае большего количества точек измерения (F, G, H и т.д.).

Где:

 - вектор остаточной вибрации в точке A.   - вектор исходной.

Математические формулы для приготовления балансировочных программ в домашних условиях.

В этом случае количество исходных уравнений становиться больше, чем количество неизвестных. Для получения однозначного решения нужно придумать что-то этакое, которое объединяло бы все неизвестные общим условием. Гаусс изобрел метод наименьших квадратов (МНК), с помощью которого можно было получать однозначные решения для специфических задач в разных областях знаний. Использовали его и балансировщики.

Корректирующие грузы, вычисленные методом наименьших квадратов, обеспечивают минимальные остаточные вибрации во всех точках измерения (в данном случае более двух). Остаточные вибрации будут разными, но минимальными для каждой индивидуальной точки.

Далее приведены формулы, с помощью которых можно в Excel составить программу вычисления балгрузов этим методом. Итак, поехали, не пугайтесь!

       (7.1)

Математические формулы для приготовления балансировочных программ в домашних условиях.

  (6.1)

  (6.2)

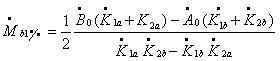
(груз во второй плоскости противоположен по фазе, сдвинут на 180 градусов)

где:

 - симметричный корректирующий (балансировочный) груз в 1-й плоскости

Математические формулы для приготовления балансировочных программ в домашних условиях.

Знаменатель в формулах (2.1) вычисляется по формуле (2.2)

Это векторная разность двух произведений, составленных из четырех векторов.

Где:

 - пробный груз при 1-ом пуске в первой плоскости

 - пробный груз при 1-ом пуске во второй плоскости

 - пробный груз при 2-ом пуске в первой плоскости

 - пробный груз при 2-ом пуске во второй плоскости

Если , то пробные грузы выбраны не корректно.

Математические формулы для приготовления балансировочных программ в домашних условиях.

Признак «качельности» объекта

(4.1.)

 - коэффициент влияния 1-й плоскости на точку А

 - коэффициент влияния 1-й плоскости на точку В  

 - коэффициент влияния 2-й плоскости на точку А  

 - коэффициент влияния 2-й плоскости на точку В