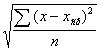Амплитуда – это величина вибрации, выраженная в единицах уровня сигнала (например, миливольты или милиамперы) или в инженерных единицах (например, микрометры или mils – один mil равен 0,001 дюйма, милиметры в секунду или дюймы в секунду и т.д.).

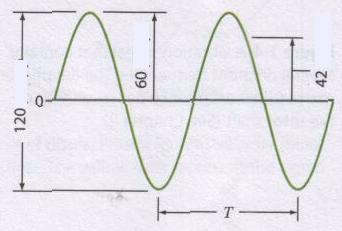
Амплитуду можно измерить несколькими способами. Один из способов: измерить общее изменение напряжения от минимума сигнала до максимума сигнала («размах»). Этот способ применяют для сигналов перемещения и называют двойная амплитуда или пик-пик, сокращенно п-п.

Рисунок 1-3. Три способа измерения амплитуды гармонического (синусоидальная волна) сигнала. Период Т представляет собой время, необходимое для одного цикла колебаний. Примечание: 120 мкм п-п; 60 мкм п-п; 42 мкм п-п.

Частота – это скорость повторения колебаний в единицу времени. Сигнал вибрации на рис.1-1 имеет только одну частоту. Частоту этого сигнала определяют путем измерения количества времени, которое требуется для совершения одного цикла колебаний (рис.1-3). Протяженность этого отрезка времени называют периодом Т; этот период показан на рисунке. Единицы измерения периода – секунды на цикл колебаний.

Частота   измеряется в циклах на секунду или в герцах (Гц) и обратно пропорциональна периоду в секундах:

   (1-1)  

Датчик вибрации – это устройство, которое преобразует механическое движение в электрический сигнал. Датчик перемещения применяют для измерения перемещения или положения объекта относительно датчика. Для большинства датчиков это – одномерное измерение, по крайней мере, в идеале.

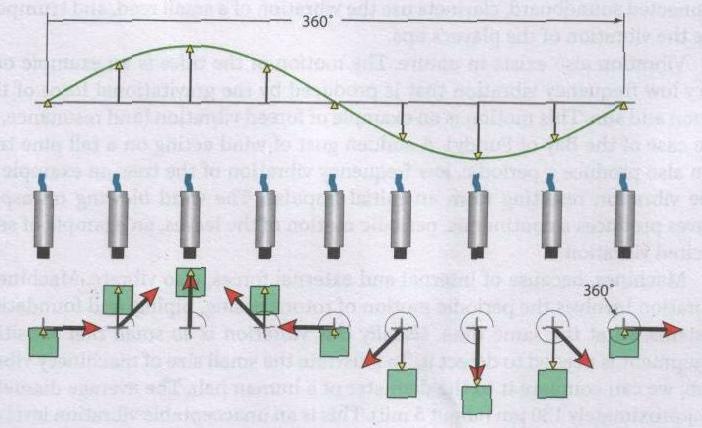
Рисунок 1-1 Соотношение движения объекта и сигнала виброперемещения. По мере движения объекта относительно измеряющего датчика возникает изменяющийся во времени сигнал напряжения. Вращающийся вектор положения, обозначенный красным цветом, вращается с круговой частотой (греческая строчная буква “омега”). Проекция этого вектора на ось датчика (показано желтым цветом) представляет собой действительное перемещение объекта.

Если объект колеблется, то его положение относительно датчика будет меняться во времени по синусоидальному закону.

ВИБРАЦИЯ – ЭТО ПЕРИОДИЧЕСКОЕ, ВОЗВРАТНО-ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ (колебание) объекта.

Ежедневно мы сталкиваемся с вибрацией самых разных видов. Почти все музыкальные инструменты для получения звука используют периодическую вибрацию механических элементов; например, в фортепиано и гитаре используется вибрация струн и соединенной с ними деки, в кларнете – вибрация маленького язычка («трость»), в трубе – вибрация губ музыканта.

Вибрация существует также и в природе. Движение приливов – это пример вибрации очень низкой частоты, которую порождает гравитационная сила луны и солнца. Это движение - пример вынужденной вибрации (и резонанса, как в заливе Фанди-Бей). Неожиданный порыв ветра, воздействуя на высокую сосну, вызывает периодические колебания дерева низкой частоты. Это - пример свободной вибрации, возникающей от начального импульса. Ветер, соприкасаясь с листвой деревьев, вызывает непрерывное, периодическое движение листьев. Это – пример самовозбуждающейся вибрации.

Выведена формула для оценки притяжения для асинхронных электродвигателей.

  (кг)

где:

 - для 2х полюсных асинхронных эл.дв.   равно 1, для 4х и более 1.5.  

 - диаметр ротора в сантиметрах

 - длина железа ротора в сантиметрах

 - величина эксцентричного смещения ротора в расточке статора

 - номинальный воздушный зазор

Математические формулы для приготовления балансировочных программ в домашних условиях.

С этих формул все началось:  

  (12.1)

где:

 - вектор исходной вибрации в точке А

 - вектор исходной вибрации в точке B

 - коэффициент влияния 1-й плоскости на точку А

 - коэффициент влияния 1-й плоскости на точку В  

Математические формулы для приготовления балансировочных программ в домашних условиях.

Известны балгрузы для 1-й и 2-й балансировочных (корректирующих) плоскостей. Допустим, по какой-то причине эти плоскости не устраивают и белгрузы необходимо перенести в другие две плоскости. Назовем их 3-й и 4-й плоскостями. Другими словами: требуется вычислить величины балгрузов при переносе их в две другие плоскости балансировки.

Формулы для вычисления балгрузов при параллельном переносе из двух плоскостей в две другие (необходимо знать коэффициенты влияния на обе точки новых плоскостей):

  (11.1)  

Где:

  (11.12)

Математические формулы для приготовления балансировочных программ в домашних условиях.

Иногда бывает очень полезно разложить полученные векторы балансировочных грузов для первой () и второй () плоскостей на симметричные и кососимметричные составляющие. Такие составляющие можно вычислить по формулам для симметричных:  

И для кососимметричных:

Где:

 - вектор балансировочного груза для 1-й корректирующей плоскости

 - вектор балансировочного груза для 2-ой корректирующей плоскости

Математические формулы для приготовления балансировочных программ в домашних условиях.

СТАДОТКЛОНП=  

Где: x – член ряда вещественных чисел в количестве «n» штук. Берутся со своим знаком. Это может быть и амплитуды векторов вибрации.

 - среднее значение всего ряда величин “x” из “n” членов.  

СТАДОТКЛОНП – название функции в Excel.

Со стандартным отклонением векторов сложнее, пока в математике не нашел этого понятия: «стандартное отклонение векторов».

Автор rotkiv

Математические формулы для приготовления балансировочных программ в домашних условиях.

Автор rotkiv